勾配消失問題

要点まとめ

ニューラルネットワークの学習がうまくいかなくなる原因の一つ。入力層に近いパラメータでは学習してもほとんど変わらない状態になる。中間層が多くなると起こりやすい。

→なぜか？中間層が多くなると誤差逆伝播における微分の回数が増える。微分値に0~1の間の数値があると、掛け合わすたびに非常に小さな数になってしまうから。

→特にシグモイド関数は、勾配消失を起こす要因となる活性化関数である。シグモイドは微分すると、最大でも0.25となる。（下記）

#シグモイド関数の実装
def sigmoid(x):
    s = 1/(1+np.exp(-x))
    return s

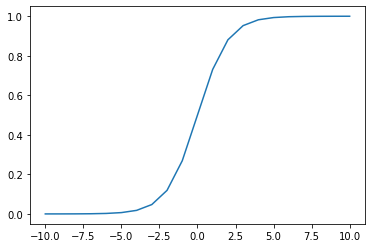
f:id:rakurakura:20220103123928p:plain

#シグモイド関数の微分
def d_sigmoid(x):
    s_d = (1-sigmoid(x))*sigmoid(x)
    return s_d

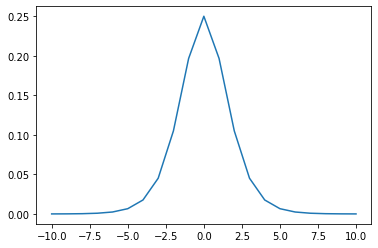
f:id:rakurakura:20220103123946p:plain

勾配消失を回避する3つの方法

活性化関数の選択：シグモイドではなく、ReLU関数を使う。
初期値を工夫する：重みパラメータ $w$ は、乱数でランダムな初期値を与えるが、この与え方を工夫することで勾配消失を回避できる。シグモイドのようなS字カーブ型の場合は、Xavierの初期値を使う。Xavierでは、重みの要素を、前層のノード数の平方根で割った値を使うことで、良い感じに微分値のばらつきと表現力が保持される。
バッチ正規化：ミニバッチの単位で、入力値のデータの偏りを抑制する手法。メリットとして、中間層の学習が安定しスピードアップする・極端なばらつきがなくなり、過学習が抑制できる。

【実装】Xavier/ He 初期値の設定方法

#Xavierの初期値
network["W1"] = np.randdom.randn(input_layer_size, hidden_layer_size) / np.sqrt(input_layer_size)
network["W2"] = np.randdom.randn(hidden_layer_size, output_layer_size) / np.sqrt(hidden_layer_size)

ReLU関数などのS字カーブではない場合は、Heの初期値設定を行うと良い。
Xavierと違うのは、 $\sqrt 2/n$ で割っているところ。

#Heの初期値
network["W1"] = np.randdom.randn(input_layer_size, hidden_layer_size) / np.sqrt(input_layer_size) * np.sqrt(2)
network["W2"] = np.randdom.randn(hidden_layer_size, output_layer_size) / np.sqrt(hidden_layer_size) * np.sqrt(2)

（メモ）重みの初期値をゼロにしてしまうと、すべての重みの値が均一に更新されてしまうので、ニューラルネットワークとして機能が果たせない点に注意。活性化関数によって初期値の与え方は使い分けるべし。

【実装】バッチ正規化レイヤー

# バッチ正則化 layer
class BatchNormalization:
    def __init__(self, gamma, beta, momentum=0.9, running_mean=None, running_var=None):
        self.gamma = gamma #スケール関数
        self.beta = beta #オフセット
        self.momentum = momentum
        self.input_shape = None

        self.running_mean = running_mean #テスト時の平均
        self.running_var = running_var  
        
        # backward時に使用する中間データ
        self.batch_size = None
        self.xc = None
        self.std = None
        self.dgamma = None
        self.dbeta = None

    def forward(self, x, train_flg=True):
        if self.running_mean is None:
            N, D = x.shape
            self.running_mean = np.zeros(D)
            self.running_var = np.zeros(D)
                        
        if train_flg:
            mu = x.mean(axis=0) # 平均
            xc = x - mu # xをセンタリング
            var = np.mean(xc**2, axis=0) # 分散
            std = np.sqrt(var + 10e-7) # スケーリング
            xn = xc / std
            
            self.batch_size = x.shape[0]
            self.xc = xc
            self.xn = xn
            self.std = std
            self.running_mean = self.momentum * self.running_mean + (1-self.momentum) * mu # 平均値の加重平均
            self.running_var = self.momentum * self.running_var + (1-self.momentum) * var #分散値の加重平均
        else:
            xc = x - self.running_mean
            xn = xc / ((np.sqrt(self.running_var + 10e-7)))
            
        out = self.gamma * xn + self.beta 
        
        return out

最適化手法

要点まとめ

勾配降下法における、 $w_{t+1} ← w_{t} - ε∇E$ のεの最適化の手法。オプティマイザーという。
学習率が大きいと発散し正解にたどり着かない。学習率が小さい場合は、大域局所最適値に収束しづらい。
モメンタム、Adagrad、RMSProp、Adamの主に4つの手法があり、昨今はAdamが定番になっている。

モメンタム

　 $V_{t} = μV_{t-1} - ε∇E$
　 $w_{t+1} = w_{t} +V_{t}$

前回の重みを考慮し、慣性の考え方を取り入れている。
最初は動きが遅いが谷間についてから最も低い位置にいくまでの時間が早く、大域局所最適値にたどり着きやすい。移動平均のようは進み方をする。

self.v[key] = self.momentum * self.v[key] -self.learning_rate * grad[key]
params[key] += self.v[key]

Adagrad

　 $h_{0} = θ$
　 $h_{t} = h_{t-1} +(∇E)^2$
　 $w_{t+1} = w_{t} -ε \cdot \frac{1}{\sqrt {h_{t}} + θ} \cdot ∇E$

これまでの学習履歴をh に蓄積させておくイメージ。
緩やかな勾配にスムーズに学習が進みやすいが、大域局最適値にたどりつきにくい。
鞍点のような状態では学習が進まなくなる。

self.h[key] = np.zeros_like(val) #なにかしらの値で初期化
self.h[key] += grad[key] * grad[key] #計算した勾配の2乗を保持しておく
params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7) #現在の重みを適応させた学習率で更新

RMSProp

　 $h_{t} = αh_{t-1} +(1-α)(∇E)^2$
　 $w_{t+1} = w_{t} -ε \cdot \frac{1}{\sqrt {h_{t}} + θ} \cdot ∇E$

Adagradの改良版。重みの更新式は同じだが、前回の経験をどの程度活かすかを調整する係数α（0~1の値 decay rate）が追加。
Adagradで難しかった鞍点問題をスムーズに解消できるようになった。
εやdecay rateは人間が最初に設定するハイパーパラメータ。

self.h[key] *= self.decay_rate #数式でのαをhにかける。
self.h[key] += (1-self.decay_rate) * grad[key] * grad[key] 
params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7) #Adagradと同じ

Adam

モメンタムとRMSPropのメリットを孕んだアルゴリズム

　 $g_{t} = ∇_{θ}f_{t} (θ_{t-1})$
　 $m_{t} = β_1 \cdot m_{t-1}+(1-β_1）\cdot g_{t}$
　 $v_{t} = β_2 \cdot v_{t-1}+(1-β_2）\cdot g_{t}^2$
　 $\hat{m_{t}} = m_{t} / (1-β_1^t)$
　 $\hat{v_{t}} = v_{t} / (1-β_2^t)$
　 $w_{t} = w_{t-1} - α \cdot \hat{m_{t}} / (\sqrt {\hat{v_{t}} }+ ε)$

 m[key] = np.zeros_like(network.params[key])
 v[key] = np.zeros_like(network.params[key])
            
 m[key] += (1 - beta1) * (grad[key] - m[key])
 v[key] += (1 - beta2) * (grad[key] ** 2 - v[key])            
 network.params[key] -= learning_rate_t * m[key] / (np.sqrt(v[key]) + 1e-7)

過学習

要点まとめ

訓練データに特化して学習してしまい、テスト誤差が収束しなくなること
原因としては、入力データ数が少ない割に大きなニューラルネットワーク（パラメータ数が多い）場合に起こり得る。パラメータ値が適切ではない（特定の重みが大きい値をとってしまっている）。ノード数が多すぎるなどが挙げられる。＝ニューラルネットワークの自由度が高すぎることが大きな要因になる。

正則化手法

過学習を抑えるアプローチとして、ニューラルネットワークの自由度に制限を与えることで対応する。過学習が起きている時、重要な重みが大きくなるが、一部の重みが極端に大きすぎることで過学習になっていることがある。そこで、重みを大きくなりすぎないような工夫としてL1、L2正則化によって、Weight Decayを実施する。

Weight Decay （重み減衰）：過学習が起こりそうな重みの大きさ以下にコントロールし、かつ重みの大きさにばらつきを出す。具体的には、誤差関数にPノルムを加える。

L1正則化：ラッソ回帰　L2正則化：リッジ回帰　では、pノルムというベクトルの距離を使う。p1ノルムではマンハッタン距離（横方向と縦方向を足すだけ）、p2ノルムはユークリッド距離（二乗して平方根する直線距離）で計算する。

重みのpノルムを計算し、誤差関数に正則化項として加えるイメージ。誤差関数の形を正則化項を足し合わせることで、変形させ、最適解の場所をずらすことで、過学習となるような最適解に陥らないようにする効果がある。

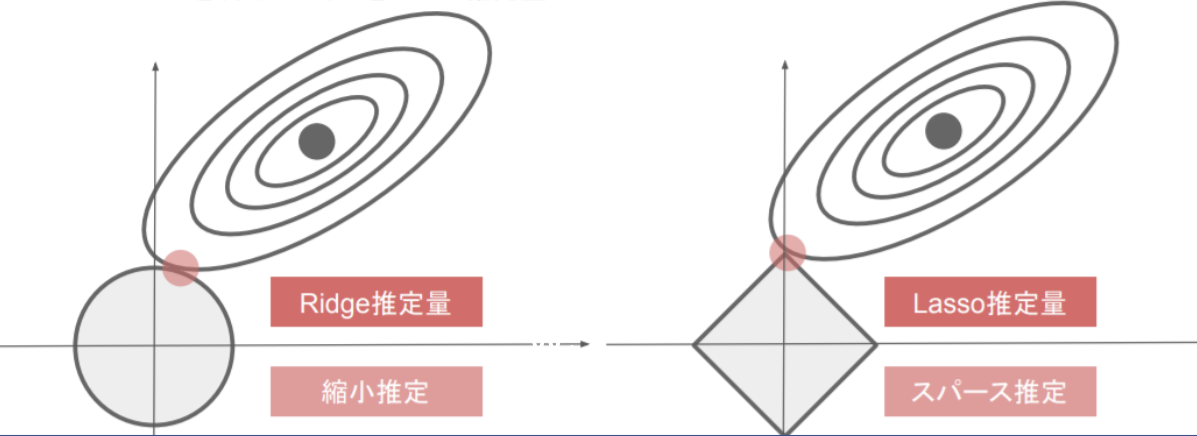
f:id:rakurakura:20220103150103p:plain

↑ 左がL2正則化、右がL1正則化
（誤差関数の等高線のイメージ）

【実装】L1正則化、L2正則化

#p1ノルムを使った正則化（L1正則化）部分抜粋
    for idx in range(1, hidden_layer_num+1):
        grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * np.sign(network.params['W' + str(idx)])
        grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
        network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
        network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]        
        weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))#絶対値をとっている

    loss = network.loss(x_batch, d_batch) + weight_decay

#p2ノルムを使った正則化（L2正則化）部分抜粋
for idx in range(1, hidden_layer_num+1):
        grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * network.params['W' + str(idx)]
        grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
        network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
        network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]        
        weight_decay += 0.5 * weight_decay_lambda * np.sqrt(np.sum(network.params['W' + str(idx)] ** 2)) #2乗の平方根をとっている

    loss = network.loss(x_batch, d_batch) + weight_decay

ドロップアウト

ノード数が多いことで過学習が起こる問題に対して、ランダムにノードを削除して学習させる手法がドロップアウト。データ量を変化させずに、異なるモデルを学習させているアンサンブル学習ともいえる。データのバリエーションを増やすことで過学習の抑止につながる。

・ドロップアウトとは異なり、ドロップコネクトという手法もあるが、これはノードは削除せずに、重みパラメータを削除することで、ノード間の接続のバリエーションを変える手法。

#ネットワークの定義
class MultiLayerNet:
    '''
    input_size: 入力層のノード数
    hidden_size_list: 隠れ層のノード数のリスト
    output_size: 出力層のノード数
    activation: 活性化関数
    weight_init_std: 重みの初期化方法
    weight_decay_lambda: L2正則化の強さ
    use_dropout: ドロップアウトの有無
    dropout_ratio: ドロップアウト率
    use_batchnorm: バッチ正規化の有無
   '''
   def __init__(self, input_size, hidden_size_list, output_size, activation='relu', weight_init_std='relu', weight_decay_lambda=0,
                 use_dropout = False, dropout_ratio = 0.5, use_batchnorm=False):
        self.input_size = input_size
        self.output_size = output_size
        self.hidden_size_list = hidden_size_list
        self.hidden_layer_num = len(hidden_size_list)
        self.use_dropout = use_dropout
        self.weight_decay_lambda = weight_decay_lambda
        self.use_batchnorm = use_batchnorm
        self.params = {}

        # 重みの初期化
        self.__init_weight(weight_init_std)

        # レイヤの生成
        activation_layer = {'sigmoid': layers.Sigmoid, 'relu': layers.Relu}
        self.layers = OrderedDict()
        for idx in range(1, self.hidden_layer_num+1):
            self.layers['Affine' + str(idx)] = layers.Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])
            if self.use_batchnorm:
                self.params['gamma' + str(idx)] = np.ones(hidden_size_list[idx-1])
                self.params['beta' + str(idx)] = np.zeros(hidden_size_list[idx-1])
                self.layers['BatchNorm' + str(idx)] = layers.BatchNormalization(self.params['gamma' + str(idx)], self.params['beta' + str(idx)])
                
            self.layers['Activation_function' + str(idx)] = activation_layer[activation]()
            
            if self.use_dropout:
                self.layers['Dropout' + str(idx)] = layers.Dropout(dropout_ratio)

        idx = self.hidden_layer_num + 1
        self.layers['Affine' + str(idx)] = layers.Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])

        self.last_layer = layers.SoftmaxWithLoss()

    def __init_weight(self, weight_init_std):
        all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
        for idx in range(1, len(all_size_list)):
            scale = weight_init_std
            if str(weight_init_std).lower() in ('relu', 'he'):
                scale = np.sqrt(2.0 / all_size_list[idx - 1])  # ReLUを使う場合に推奨される初期値
            elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
                scale = np.sqrt(1.0 / all_size_list[idx - 1])  # sigmoidを使う場合に推奨される初期値
            self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
            self.params['b' + str(idx)] = np.zeros(all_size_list[idx])

    def predict(self, x, train_flg=False):
        for key, layer in self.layers.items():
            if "Dropout" in key or "BatchNorm" in key:
                x = layer.forward(x, train_flg)
            else:
                x = layer.forward(x)

        return x

    def loss(self, x, d, train_flg=False):
        y = self.predict(x, train_flg)

        weight_decay = 0
        for idx in range(1, self.hidden_layer_num + 2):
            W = self.params['W' + str(idx)]
            weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W**2)

        return self.last_layer.forward(y, d) + weight_decay

    def accuracy(self, X, D):
        Y = self.predict(X, train_flg=False)
        Y = np.argmax(Y, axis=1)
        if D.ndim != 1 : D = np.argmax(D, axis=1)

        accuracy = np.sum(Y == D) / float(X.shape[0])
        return accuracy

    def gradient(self, x, d):
        # forward
        self.loss(x, d, train_flg=True)

        # backward
        dout = 1
        dout = self.last_layer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 設定
        grads = {}
        for idx in range(1, self.hidden_layer_num+2):
            grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.params['W' + str(idx)]
            grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db

            if self.use_batchnorm and idx != self.hidden_layer_num+1:
                grads['gamma' + str(idx)] = self.layers['BatchNorm' + str(idx)].dgamma
                grads['beta' + str(idx)] = self.layers['BatchNorm' + str(idx)].dbeta

Dropoutのクラスを生成する

#Dropoutのクラスを生成
class Dropout:
    def __init__(self, dropout_ratio=0.5):
        self.dropout_ratio = dropout_ratio
        self.mask = None

    def forward(self, x, train_flg=True):
        if train_flg:
            self.mask = np.random.rand(*x.shape) > self.dropout_ratio
            return x * self.mask
        else:
            return x * (1.0 - self.dropout_ratio)

    def backward(self, dout):
        return dout * self.mask

use_dropout = True
dropout_ratio = 0.15

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10, weight_decay_lambda=weight_decay_lambda, use_dropout = use_dropout, dropout_ratio = dropout_ratio)

2022-01-03

E資格学習　深層学習 Day1

さて、今回は深層学習の基礎と概要について要点をまとめたいと思います。

入力層～中間層
活性化関数
出力層
- 要点まとめ
誤差関数
【実装】2×3×3×1のニューラルネットワークの実装
勾配降下法
誤差逆伝播法（Back Propagation）
- 要点まとめ
- 【実装】

入力層～中間層

要点まとめ
・結局、ディープラーニングは何をやろうとしているのか
　→入力値から目的となる出力値を導く「関数」or「数理モデル」を自動的に学習して構築する仕組み
　　重み[W]とバイアス[b]の最適化が最終目的。

・（例）例えば、最終的に、猫、犬、ねずみといった動物分類を考える。
　　　　入力値：体長、体重、ひげの本数、毛の平均長、耳の大きさ・・・etc
　　　　出力値：猫、犬、ねずみといった各正解ラベルに該当する確率

・（例）入力層：2ノード、中間層：3ノード×2層、出力層：1ノードのNN
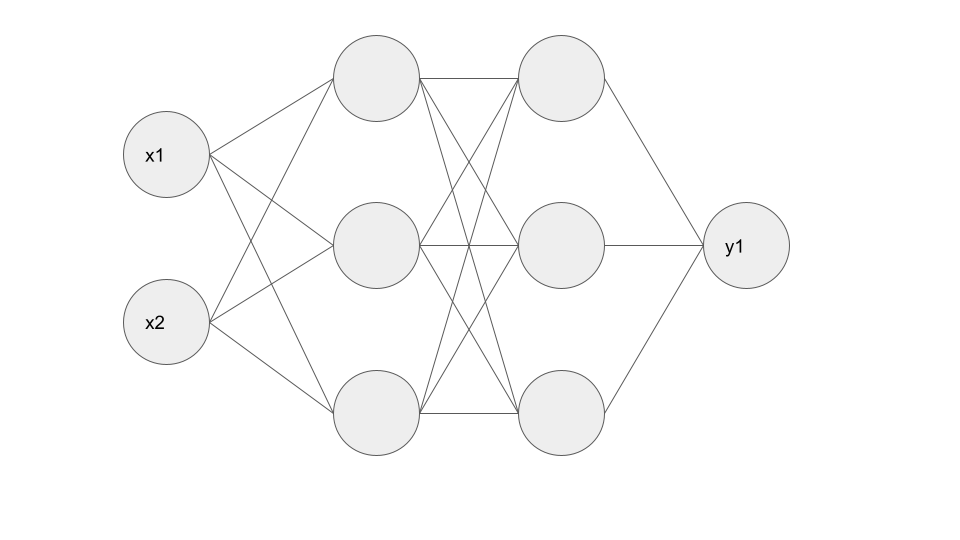
　　　　 f:id:rakurakura:20220103002312p:plain

活性化関数

要点まとめ

・ニューラルネットワークは非線形の関数であるため複雑な分類・識別タスクに強い。その大きな要因となっているのが活性化関数の存在。
・活性化関数があるおかげで、一部の出力が強く、一部の出力が弱く伝播される。
・主に中間層用の活性化関数：RELU関数、ステップ関数　etc
・主に出力層用の活性化関数：シグモイド関数、ソフトマックス関数　etc

STEP関数

・閾値を超えたら発火する。xがゼロ以上であれば1、そうでなければゼロを返す。
・昨今はあまり使われない。

def step_func(x):
　if x>0:
       return 1
    else:
       return 0

シグモイド関数

・非線形な活性化関数。線形のような直線ではなく、非線形
・値がなだらかな曲線なので、微分が可能。
　ただし、複雑になると、勾配消失問題を引き起こす原因になるため、
　中間層ではあまり使われない。

def sigmoid(x):
  return 1/(1+np.exp(-x))

RELU関数

・ゼロよりも小さい場合はゼロを、大きい場合は入力値をそのまま出力する
・勾配消失を回避できる。

def relu(x):
  return np.maximum(0, x)

Softmax関数

def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T
    x = x - np.max(x) # オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x))

出力層

要点まとめ

・最後の出力層は、人間が欲しい答えに該当する数値（回帰であれば実数値、分類であれば正解ラベルの確率）が出力させる必要がある。

・出力層で使う活性化関数は、中間層で扱う活性化関数のように、特徴抽出ではなくより人間が最終的に扱いやすいように変形させる、という特徴があるため、両者で用いる関数が異なる。

誤差関数

要点まとめ

・出力層で得た出力値と、事前に用意した正解値との差を誤差関数と定義し、この誤差関数を最小化するように最適なパラメータを探索する計算処理→これがNNにおける「学習」そのものである。

・誤差関数を計算する際に、誤差を2乗する理由は？
　→各データと正解との誤差を計算する際に、正負の値が発生すると相殺して全体的な誤差を正しく表現できないため、2乗して正の値として扱うことで正負の相殺を回避する。

・誤差関数を計算する際に、1/2を掛けている理由は？
　→本質的な理由ではなく、便宜上、誤差関数を微分する際に出てくる2を打ち消す効果として1/2をかけている。

・分類問題で使う誤差関数：クロスエントロピー誤差
・回帰問題で使う誤差関数：MSE（平均二乗誤差）

MSE

# 平均二乗誤差
# dが教師データ、yが予測データ
def mean_squared_error(d, y):
    return np.mean(np.square(d - y)) / 2

クロスエントロピー

# dが教師データ、yが予測データ
def cross_entropy_error(y, d):
    # log 0回避用の微小な値を作成
    delta = 1e-7
    
    # 交差エントロピー誤差を計算
    return - np.sum(d* np.log(y + delta))

Softmax関数＋クロスエントロピー

#ソフトマックスとクロスエントロピー誤差の複合関数
def d_softmax_with_loss(d, y):
    batch_size = d.shape[0]
    if d.size == y.size: # 教師データがone-hot-vectorの場合
        dx = (y - d) / batch_size
    else:
        dx = y.copy()
        dx[np.arange(batch_size), d] -= 1
        dx = dx / batch_size
    return dx

【実装】2×3×3×1のニューラルネットワークの実装

イメージ
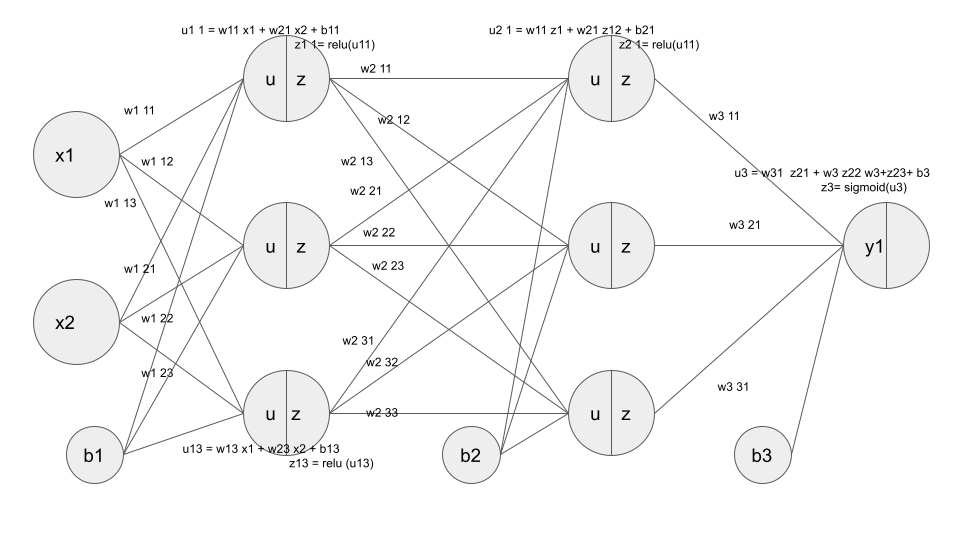
f:id:rakurakura:20220103020050p:plain

#2値分類
#上記に記載した入力層：2層、中間層：3層×2、出力層：1のネットワークを作成する

#シグモイド関数
def sigmoid(x):
    return 1/(1 + np.exp(-x))

#シグモイド関数の微分
def d_sigmoid(x):
    dx = (1.0 - sigmoid(x)) * sigmoid(x)
    return dx

# ReLU関数
def relu(x):
    return np.maximum(0, x)

#ReLU関数の微分
def d_relu(x):
    return np.where( x > 0, 1, 0)


#クロスエントロピー誤差
def cross_entropy_error(d, y):
    if y.ndim == 1:
        d = d.reshape(1, d.size)
        y = y.reshape(1, y.size)
        
    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
    if d.size == y.size:
        d = d.argmax(axis=1)
             
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size


#ネットワークの定義
def init_network():
    network = {}
    network['W1'] = np.random.rand(2, 3)
    network['W2'] = np.random.rand(3, 3)
    network['W3'] = np.random.rand(3, 1)

    network['b1'] = np.random.rand(3)
    network['b2'] =np.random.rand(3)
    network['b3'] =np.random.rand(1)

    return network

#ネットワーク
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'],network['W3']
    b1, b2, b3 = network['b1'], network['b2'],network['b3']

    # 隠れ層の総入力
    u1 = np.dot(x, W1) + b1

    # 隠れ層1の総出力
    z1 = relu(u1)

    # 隠れ層２層への総入力
    u2 = np.dot(z1, W2) + b2

    # 隠れ層2の出力
    z2 = relu(u2)
    
    u3 = np.dot(z2, W3) + b3
    z3 = sigmoid(u3)

    y = z3    
    
    return y, z1

# 入力値
x = np.array([1., 2.])

# 目標出力
d = np.array([1])
network =  init_network()
y, z1 = forward(network, x)
# 誤差
loss = cross_entropy_error(d, y)

勾配降下法

要点まとめ

・深層学習でパラメータを最適化するために用いられる手法＝勾配降下法
・通常の勾配降下法は、バッチ学習のようにデータを全て準備し、全て使って学習するイメージ。パラメータの更新式は、 $w_{t+1} = w_{t} - ε∇E$ で表される。
・バリエーションとして、確率的勾配降下法（SGD）とミニバッチ勾配降下法がある。
・バッチ処理なので、大量のデータを扱う際には、かなり計算コストが高くなる。

確率的勾配降下法

・バッチ学習とは異なり、オンライン学習（学習データが入ってくるたびに、都度パラメータを更新し学習を進めていく方法）
・ $w_{t+1} = w_{t} - ε∇E_{n}$ で表される。（Eの添字にnが入っている点がバッチ学習と違うところ！）

ミニバッチ勾配降下法

・確率的勾配降下法のメリットを損なわず、大量のデータを「小分け」することで扱えるようにした手法。この小分けにしたデータ集合をミニバッチと呼ぶ。
・10万枚を500枚ずつに小分けすると2000個のバッチができあがる。
・500枚単位での誤差が2000個分集まると2000で割ることで平均的な誤差が求まる。
・小分けしたデータを並列処理することで、バッチ処理とは異なり計算資源を有効利用できるメリットもある。（SIMD並列化：single instruction multi data）
$w_{t+1} = w_{t} - ε∇E_{t}$ で表される。

学習のイメージ

・エポックの進行：t → t+1 → t+2 とすると、
・重みの値　： $w_t → w_{t+1} → w_{t+2}$ と変化する
・変化量　　： $-ε∇E_{t} → -ε∇E_{t+1}$

誤差逆伝播法（Back Propagation）

要点まとめ

・上記のような、重みの更新の際に必要となる∇Eをどのように求めるのか？
→誤差関数の微分を用いることで更新できるが、重みの数が膨大になると微分の計算も膨大になり負荷が大きくなるので、数値微分だと限界。そこで、微分の連鎖律の性質を活用することで、「解析的に」計算することができる誤差逆伝播法が用いられる。

【実装】

# 誤差逆伝播
def backward(x, d, z1, y):
    grad = {}
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']

    # 出力層でのデルタ（Eをyで微分したもの）
    delta2 = mean_squared_error(d, y)

    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)

    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)

    # 出力層でEをyで微分した結果「delta2」と、yをuで微分した結果を掛けている
    delta1 = np.dot(delta2, W2.T) * d_sigmoid(z1)

    delta1 = delta1[np.newaxis, :]

    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    x = x[np.newaxis, :]

    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)
    
　return grad

$\frac {∂E}{∂y} \cdot \frac {∂y}{∂u}$ の部分は以下のコードで表している。

delta1 = np.dot(delta2, W2.T) * d_sigmoid(z1)

2022-01-02

E資格学習　機械学習まとめ

線形回帰問題
非線形回帰問題
ロジスティック回帰問題
主成分分析
- 要点まとめ
- 【実装】サンプル100個のデータを次元圧縮する
サポートベクターマシン
- 要点まとめ
- 【実装】SVMでの分類器を作る

線形回帰問題

要点まとめ

・教師あり学習の1つ。ある入力から出力（目的変数）を予測する際に「直線」で予測するものを線形回帰という。（曲線の場合は非線形回帰という）
・入力xは、説明変数・特徴量とも呼ばれる。xはm次元のベクトルであり、出力yはスカラー値となる。
・説明変数xが1つのとき線形単回帰、複数の場合は線形重回帰と呼ぶ。
　（＝つまり、1つの変数を使って予測するか複数の変数で予測するかの違いである）
・出力値は、入力xに対して重みパラメータw（xと同じくm次元のベクトル）を掛け合わせて以下の式で表される。

（補足）最小二乗法

・線形回帰では予測した直線と真のデータの距離（残差）の平方和（平均二乗誤差＝残差平方和）から、その残差平方和が最小となるパラメータを探索する方法で最適解を見つける、最小二乗法が主に用いられる。
（やろうと思えば、最尤推定でも解ける）
・最小二乗法では、MSE を微分してゼロになる点が最適なパラメータとなる（平均二乗誤差の勾配が0）
・パラメータwは、式を見てわかる通り、XとYさえわかれば探索的に求めることができる。

（補足）ホールドアウト法

・機械学習では、学習用と検証用で使用するデータは変える。
　→なぜか？　汎化性能を測りたいから。未知のデータにどれくらい精度が出るかを確認したいため。
・ホールドアウト法は、ある有限のデータを、学習用とテスト用の2つに分割する方法（例えば80%学習用、20%検証用）
・ただし、学習用のデータを多くすると評価用が少なくなってしまうため、十分なデータ量が必要になってしまう点が注意。

（補足）クロスバリデーション（交差検証法）

・データを学習用と評価用に分割する点は、ホールドアウトと同じ。
・ホールドアウトと違うのは、データをn分割し、そのうち1つ（1/n）を検証データ、その他(1-1/n)を学習データとして、学習用と評価の組み合わせをnパターン作り、評価を全てのパターンで繰り返して、平均値で評価する方法。

【実装】ボストンの住宅価格を予測する

データの準備

#必要なライブラリをインポートする
#sklearnには、予めボストンの住宅価格データセットがJSON形式で用意されている
from sklearn.datasets import load_boston
from pandas import DataFrame
import numpy as np

# ボストンデータを"boston"というインスタンスにインポート
boston = load_boston()

#説明変数をDataFrameへ変換
df = DataFrame(data=boston.data, columns = boston.feature_names)

単回帰の場合（部屋の広さから価格を予測する場合）

# 説明変数　部屋数のみを指定
data = df.loc[:, ['RM']].values
# 目的変数　金額を指定
target = df.loc[:, 'PRICE'].values

## sklearnモジュールからLinearRegressionをインポート
from sklearn.linear_model import LinearRegression
# オブジェクト生成
model = LinearRegression()
# fit関数でパラメータ推定
model.fit(data, target)

#予測　6部屋の場合の金額を出力する
model.predict([[6]])

重回帰の場合（犯罪率と部屋数から金額を予測する場合）

# 説明変数
data2 = df.loc[:, ['CRIM', 'RM']].values
# 目的変数
target2 = df.loc[:, 'PRICE'].values

# オブジェクト生成
model2 = LinearRegression()
# fit関数でパラメータ推定
model2.fit(data2, target2)

#犯罪率と部屋数を入力する
model2.predict([[0.2, 7]])

非線形回帰問題

要点まとめ

・xにおける線形モデルでは、直線（1次関数）での予測なので、表現力が制限されていたが、xに曲線の成分（2次関数、三角関数、対数関数など）が含まれることで、非線形な問題を予測できるようになる。
・そこで、説明変数 $x$ について、高次のxをまとめて基底関数： $φ(x)$ に変換して表現する。
・基底関数としてはガウス型基底関数、多項式関数（ $φ_j = x^j$ ）等があるが、説明変数xをこの基底関数で変換した後の（ $φ(x)$ ）に、重みパラメータと線形結合してyを出力する。
・つまり、あくまでxが非線形になったモデルなだけであって、重みパラメータ $w$ については線形のままという点は注意。

（補足）よく使われる基底関数

・ガウス型基底関数
・多項式関数
・スプライン関数

（補足）過学習（overfitting）と未学習（underfitting）

・過学習の例：例えば4次の曲線で十分なのに、より高次な9次の曲線で回帰した場合　等
・見学習の例：例えば4次の曲線が適切なのに、2次の曲線で回帰してしまった場合

・一般的には、基底関数の数を多くすればするほど過学習になりやすい。そこで、基底関数が多くても正則化項を入れることで、汎化性能を保つことができるようになる。

（補足）正則化（L1正則化+L2正則化）

・過学習を抑止するために、目的関数に罰則項を設ける方法。MSEだけでなくモデルが複雑になると大きくなるような罰則項を、MSEに加える。そうすることで、MSEだけを小さくしても、罰則項が大きくなるので、モデルが複雑になり過学習になるのを防ぐことができる。

・L1正則化（ラッソ正則化）：いくつかのパラメータが0になる。スパース推定。
・L2正則化（リッジ正則化）：パラメータが0に近づくが、完全には0にならない。

・正則化項の影響度合は、 $γ$ で調整する。

（補足）グリッドサーチ

・全てのチューニングパラメータの組み合わせで、評価する方法。
・最近はベイズ最適化などが使われている。

【実装】非線形ノイズデータを予測する

0. 事前準備

#必要なライブラリをインポートしておく
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

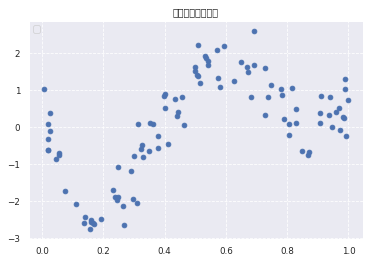
1.データの生成

#ランダムに100個のデータを生成
n=100
# 関数を使ってデータ生成
def true_func(x):
    z = 1-48*x+218*x**2-315*x**3+145*x**4
    return z 
def linear_func(x):
    z = x
    return z 

# 上記の関数を使ってデータ生成
data = np.random.rand(n).astype(np.float32)
data = np.sort(data)
target = true_func(data)

# ノイズを加える
noise = 0.5 * np.random.randn(n) 
target = target  + noise

# ノイズ付きデータを描画
plt.scatter(data, target)
plt.title('NonLinear Regression')
plt.legend(loc=2)

f:id:rakurakura:20220102185133p:plain — sample

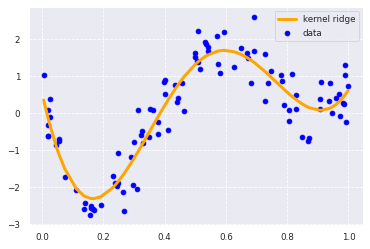
2. sklearnで非線形に予測する

from sklearn.kernel_ridge import KernelRidge

data = data.reshape(-1,1)
target = target.reshape(-1,1)

clf = KernelRidge(alpha=0.0002, kernel='rbf')
clf.fit(data, target)

p_kridge = clf.predict(data)

plt.scatter(data, target, color='blue', label='data')

plt.plot(data, p_kridge, color='orange', linestyle='-', linewidth=3, markersize=6, label='kernel ridge')
plt.legend()
#plt.plot(data, p, color='orange', marker='o', linestyle='-', linewidth=1, markersize=6)

f:id:rakurakura:20220102185431p:plain — nonlinear

ロジスティック回帰問題

要点まとめ

・2値のクラス分類問題を扱うときに用いる手法。
・ロジスティック線形回帰モデルでは、説明変数xとパラメータwの線形結合したものを、さらにシグモイド関数σに入力することで、最終的に0~1の数値で出力する。これは、y=1となる確率値としてみなせる。
・ $P(Y=1 | x) = σ(w_0 + w_1x_1 + w_2x_2 + \cdots + w_nx_n)$ となるようなモデルを作ることが、ロジスティック回帰の目的。（翻訳すると、xを与えた時のY=1となる確率を求める）
・目的変数y は0か1かに分類する。

（補足）シグモイド関数

・入力は実数→出力値は0〜1となる
・シグモイド関数→ $σ(x)=\frac {1}{1+exp(-ax)}$
・aを増加させると、x=0付近の勾配が増加する
・シグモイド関数の微分　→ $\frac {∂σ(x)}{∂x} = aσ(x)(1-σ(x))$ となる
・pythonでシグモイド関数を実装してみると以下の通りになる。

　def sigomid(x):
　　　s = 1/1+np.exp(-x)
　　　return s

（補足）最尤推定と尤度関数

・データが手元にあるとき(yの結果値）、そのデータがどのような分布から生成されたのかを推定するのがモデル作成のイメージ。
・尤度関数を最大化するようなパラメータを選ぶ推定方法を、「最尤推定」という。
・負の対数尤度関数にする理由：確率値を何度も掛け合わせることによる桁落ちを防ぐため＋微分の計算が楽＋最小化を意味させるためにマイナスをとる。

（補足）勾配降下法と確率的勾配降下法

・シグモイド関数の場合、解析的にパラメータを算出できないため、少しずつ最適解に近づいていくような、勾配降下法が用いられる。

・普通の勾配降下法（最急降下法）は、全てのデータに対する目的関数を計算してからパラメータを更新するが、確率的勾配降下法では、ランダムに1つのデータの目的関数を計算してからパラメータを更新する。（つまり、バッチ学習の最急降下法をオンライン学習に改良したものといえる。）

【実装】タイタニックの生存者予測

01. 準備（kaggle等からデータをダウンロードしておく）

#必要なライブラリをインストール
import pandas as pd
from pandas import DataFrame
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

# titanic data csvファイルの読み込み
titanic_df = pd.read_csv('titanic_train.csv')

02. ロジスティック回帰のモジュールをインポートし、インスタンスを作成

#sklearnからロジスティック回帰のモジュールをインポートする
from sklearn.linear_model import LogisticRegression
#インスタンスを生成
model=LogisticRegression()

03. 説明変数とラベル（クラス＝目的変数）を選択してフィットさせる。
ここでは、data1 に"Fare"の1変数のみを格納しlabelには"Survived"のデータを入れている。
運賃から、生死を判別する場合はこれだけで分類モデルは作成できる。
（もちろん、実際には自分自身で複数の変数を使い、特徴量エンジニアリングによって新しい特徴量を作るなどの工夫する必要がある。）

#運賃だけのリストを作成
data1 = titanic_df.loc[:, ["Fare"]].values

#生死フラグのみのリストを作成
label1 =  titanic_df.loc[:,["Survived"]].values

#モデルにフィットさせる。これでモデルが作成できる。
model.fit(data1, label1)

主成分分析

要点まとめ

・高次元のデータを低次元に圧縮する手法。
・線形変換後のデータの分散が最大になるような軸で低次元化する。

【実装】サンプル100個のデータを次元圧縮する

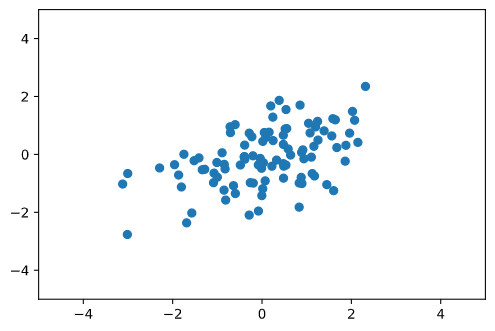
01. データを生成する

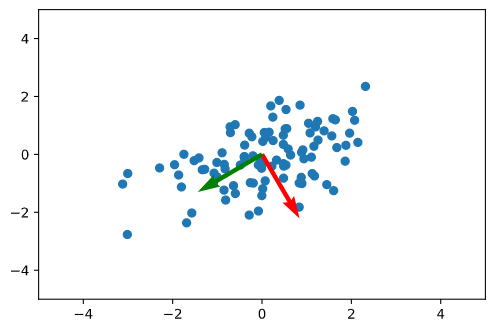
n_sample = 100

def gen_data(n_sample):
    mean = [0, 0]
    cov = [[2, 0.7], [0.7, 1]]
    return np.random.multivariate_normal(mean, cov, n_sample)

def plt_data(X):
    plt.scatter(X[:, 0], X[:, 1])
    plt.xlim(-5, 5)
    plt.ylim(-5, 5)

X = gen_data(n_sample)
plt_data(X)

f:id:rakurakura:20220102212341p:plain

訓練データ $X = [\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, ..., \boldsymbol{x}_{n}$ ^{\mathrm{T}}$に対して$\mathbb{E}[\boldsymbol{x}] = \boldsymbol{0}] となるように変換する。

すると、不偏共分散行列は $Var[\boldsymbol{x}$ = \frac{1}{n-1} X^{\mathrm{T}}X]と書ける。

n_components=2

def get_moments(X):
    mean = X.mean(axis=0)
    stan_cov = np.dot((X - mean).T, X - mean) / (len(X) - 1)
    return mean, stan_cov
    
def get_components(eigenvectors, n_components):
#     W = eigenvectors[:, -n_components:]
#     return W.T[::-1]
    W = eigenvectors[:, ::-1][:, :n_components]
    return W.T

def plt_result(X, first, second):
    plt.scatter(X[:, 0], X[:, 1])
    plt.xlim(-5, 5)
    plt.ylim(-5, 5)
    # 第１主成分
    plt.quiver(0, 0, first[0], first[1], width=0.01, scale=6, color='red')
    # 第２主成分
    plt.quiver(0, 0, second[0], second[1], width=0.01, scale=6, color='green')

#分散共分散行列を標準化
meean, stan_cov = get_moments(X)
#固有値と固有ベクトルを計算
eigenvalues, eigenvectors = np.linalg.eigh(stan_cov)
components = get_components(eigenvectors, n_components)

plt_result(X, eigenvectors[0, :], eigenvectors[1, :])

f:id:rakurakura:20220102212657p:plain

サポートベクターマシン

要点まとめ

・SVMは教師あり学習の手法の一つである。
・分類にも回帰にも使われるが、2値分類に使われることが多い。
・同じく2値分類に使われるロジスティック回帰のような確率的に出力する分類器とは異なり「決定的な出力をする分類器」といえる。
・データ点のxを $y=wtφ(x)+b$ の正負によって分類する（→このyが、クラスを分離する境界となるイメージ。）
・この境界との最短距離をマージンと呼び、SVMでは、マージンが最大となるような境界を学習する。
・ハードマージンSVM（データの誤分類を許容しない）では、マージン上のデータ点をサポートベクトルという。ちなみに、ソフトマージンSVM（データの誤分類を許容する）では、マージン内部またはご分類されたデータ点を指すことになる。
・ソフトマージンSVMで用いられるスラック変数とは、データがマージン内または誤分類された時に正の値をとる変数。
・線形カーネルでは、元のデータ空間での線形分離しかできない。非線形分離する際には、RBFカーネル（ガウシアンカーネル）、多項式カーネル、シグモイドカーネル等を用いて、特徴空間上で線形分離するアプローチを検討する。

【実装】SVMでの分類器を作る

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

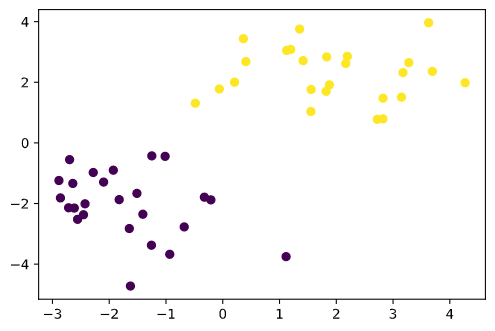
#データを生成する
def gen_data():
    x0 = np.random.normal(size=50).reshape(-1, 2) - 2.
    x1 = np.random.normal(size=50).reshape(-1, 2) + 2.
    X_train = np.concatenate([x0, x1])
    ys_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
    return X_train, ys_train

X_train, ys_train = gen_data()
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)

f:id:rakurakura:20220102213718p:plain

t = np.where(ys_train == 1.0, 1.0, -1.0)

n_samples = len(X_train)
# 線形カーネル
K = X_train.dot(X_train.T)

eta1 = 0.01
eta2 = 0.001
n_iter = 500

H = np.outer(t, t) * K

a = np.ones(n_samples)
for _ in range(n_iter):
    grad = 1 - H.dot(a)
    a += eta1 * grad
    a -= eta2 * a.dot(t) * t
    a = np.where(a > 0, a, 0)

index = a > 1e-6
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]

term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()

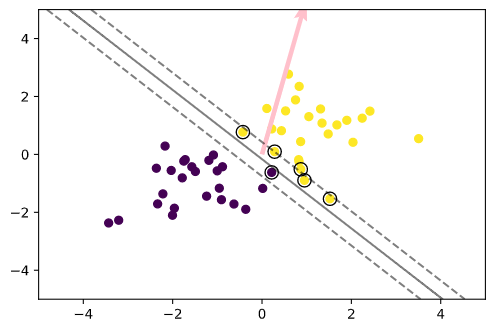
# 訓練データを可視化
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)
# サポートベクトルを可視化
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
                    s=100, facecolors='none', edgecolors='k')
# 領域を可視化
#plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
# マージンと決定境界を可視化
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
                     levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])


# マージンと決定境界を可視化
plt.quiver(0, 0, 0.1, 0.35, width=0.01, scale=1, color='pink')

f:id:rakurakura:20220102213558p:plain

2021-12-30

E資格学習　応用数学③ 情報理論　基礎まとめ

E資格取得に向けた学習として要点をまとめます。今回のテーマは「応用数学」ということで「線形代数」「確率・統計」「情報理論」の3分野について、要点とキーワード、pythonでの実装コードをまとめていきたいと思います。

情報理論

情報理論

自己情報量

情報量とは「ある事象が起きた時にどのくらい珍しい事象か」という尺度
つまり、珍しい事象（確率が小さい）ほど、情報量が多くなる性質をもつ = 驚きの度合い

自己情報量は以下の式で表される。
自己情報量 $\boldsymbol{I(x) = - \log (P(x))}$
（補足）P(x):確率分布

シャノンエントロピー

平均情報量ともよばれる。自己情報量の期待値のこと。
平均情報量＝E（自己情報量）
平均情報量 $\boldsymbol{H(x) = - E_{x-P} \log (P(x)}$ P(x):確率分布

KL（カルバックライブラー）ダイバージェンス

２つの確率分布を比較する量。
正しい分布Pに従って出てきた出力をみて、それがQではなくPだと知った時に得られる情報量の期待値（不確かさの修正度合いとも言える）

$\boldsymbol{D_{KL}(P||Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}}$

（例）あたりの確率が1/2だと思っていたが、実はあたりの確率が1/4であった場合

$\boldsymbol{D = 1/4 \log (1/4 / 1/2) + \log (3/4 / 1/2) = -1 + 3/4 \log3 }$

交差エントロピー

・KLダイバージェンスの一部分を取り出したもの
・Qの自己情報量をPの分布で平均している

$\boldsymbol{H(P,Q)=−E_{X～P} \log Q(x)= \sum_{x}P(x)logQ(x)}$

2021-12-30

E資格学習：応用数学② 確率・統計基礎まとめ

確率・統計

確率・統計

ベイズの定理（ベイズ則）

（例）受け取ったメールに含まれている特定の文字から、それがスパムメールである確率がどのくらいか。
　・メールに特定の文字が含まれている確率・・・P(A) （→周辺尤度）
　・全メールにおけるスパムメールの確率・・・P(B) （→事前確率）
　・スパムメールに、特定の文字が含まれている確率・・・P(A|B) （→尤度）とすると

　ベイズの定理より、以下となる。
　　 $\boldsymbol{P(B|A) = P(B)P(A|B)/P(A)}$

条件付き確率

（例）雨が降っている条件下で、交通事故に遭う確率
　・雨が降る確率・・・P(A)
　・交通事故に遭う確率・・・P(B) とすると
　
　条件付き確率では、以下となる。
　　 $\boldsymbol{P(B|A) = P(A \cap B )/P(A)}$

期待値・分散・共分散・標準偏差

・期待値
　ある確率分布に従う事象に対し、試行によって確率的に得られるであろう期待される値のこと

　　 $\boldsymbol{E(X) = \sum _{i=1} ^{N} {X_iP(X_i)}}$

・分散
　データの散らばり度合いを示している。標準偏差は分散の平方根となる

　　標本分散（サンプルのばらつきを表現する場合）
　　　 $\boldsymbol{s^2 = 1/n \sum _{i=1} ^{n} {(x_i-\bar{x})^2}}$

　　母分散（母集団のばらつきを表現する場合）
　　　 $\boldsymbol{Var(X) = \sum _{i=1} ^{N} {(X_i-E(X))^2 P(X_i)}}$

　　また、分散は期待値のみで表現することも可能である
　　　 $\boldsymbol{Var(X) = E(X^2) - E(X)^2}$

・共分散
　2つのデータの分布の類似度、互いの影響度がわかる指標。

　　　 $\boldsymbol{Cov(X, Y ) = E(XY) - E(X)E(Y)}$

様々な確率変数

・質的変数
・名義尺度：性別、色など（数値に意味はなくカテゴライズするために数値をあてがって分類しているもの）
・順序尺度：成績の5段階評価、満足度調査など（名義尺度＋数値に大小の意味を持たせている）

・量的変数
・間隔尺度：摂氏での気温偏差値（0に絶対的な意味がなく、相対的な意味しかないもの）
・比例尺度：身長、年齢、値段（0に絶対的な意味をもつもの）

様々な確率分布

・ベルヌーイ分布
1回の試行で成功・失敗を考えた時に、成功確率が従う分布
（例）コイン投げ、手術の成功、試合の勝敗、奇数か偶数か　etc...

　ベルヌーイ分布に従うことを、 $\boldsymbol{X〜B(1, p)}$ と表現する。
　　 $\boldsymbol{P(X=1)=p}$ のとき、
　　　ベルヌーイの確率関数 $\boldsymbol{P(x|p) = p^x(1-p)^{1-x}}$
　　　ベルヌーイの期待値 $\boldsymbol{E(X) = p}$
　　　ベルヌーイの分散 $\boldsymbol{Var(X) = p(1-p)}$ と表すことができる

・二項分布
ベルヌーイ分布をn回試行した時、その成功回数が従う分布
（例）試合の勝利合計回数、シュートの成功回数、講義の出席回数、手術の累計成功回数、etc...

　二項分布に従うことを、 $\boldsymbol{X〜B(n, p)}$ と表現する。
　　　二項分布の確率関数 $\boldsymbol{P(x|p, n) = (n x)p^x(1-p)^{n-x}}$
　　　二項分布の期待値 $\boldsymbol{E(X) = np}$
　　　二項分布の分散 $\boldsymbol{Var(X) = np(1-p)}$ と表すことができる

・ガウス分布
　正規分布ともいう。様々な自然現象が従うことの多い分布。平均μ、分散σの値が決まれば正規分布が決定する。
　平均0、分散1の正規分布を標準正規分布という
　（例）身長、体重の分布、テストの点数の分布、ウィルスの感染確率など

　ガウス分布に従うことを、 $\boldsymbol{X〜N(μ, σ^2)}$ と表現する。
　　　ガウス分布の確率関数　 $f(x)=\dfrac{1}{\sqrt{2\pi\sigma}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})$

・マルチヌーイ分布
カテゴリカル分布ともいう。1回の試行で複数の結果が確率的に発生するとき
（例）サイコロを投げた時、日本人の好きな髪型、複数のあたりがある宝くじを1回引いた時の結果　etc...

2021-12-30

E資格学習：応用数学① 線形代数　基礎まとめ

線形代数

線形代数

スカラー・ベクトル・行列・テンソル

スカラー：いわゆる普通の数。0階のテンソルともいう。
（例） $a = 2$

a= 2

ベクトル：順番に並んだ数値。大きさと向きを合わせ持つ。2値以上の数値で表現されるので、空間的な「位置」＝「向き」が表現できる。1階のテンソルともいう。横向きに書くと横ベクトル、縦方向に書くと縦ベクトルという。
（例）横ベクトル
$\vec{a} = (1, 2, 3)$ , $\vec{b} = (1, 2, \cdots, 80)$

import numpy as np
a= np.array([1, 2, 3])
b =np.arange(1, 81, 1) #arange関数を使って始点、終点、交差を指定する書き方

行列：ベクトルを表の形式にしたもの。連立方程式を解く過程で生まれた。行方向（横）、列方向（縦）に数値が並ぶ。2階のテンソルともいう。n×m行列の場合、行数n、列数mの行列を指す。
（例）2×3行列

$\boldsymbol{A} =\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}$

import numpy as np
a= np.array([[1, 2, 3],[4, 5, 6]])

テンソル：行列はタテ・ヨコの2次元だが、さらに3次元以上に並べた数列。タテ・ヨコ方向だけでなく奥行き方向等（ただし、4次元以上になると空間的な表現難しい）。3階のテンソル、4階のテンソルのように表現する。

import numpy as np
a = np.array([[[1, 2],[3,4]],[[5,6],[7,8]], [[9,10],[11,12]]]) #3次元
b = np.arange(1,25,1).reshape(2,3,2,2)  #24個の1次元配列を4次元テンソル（2行2列×3次元のテンソルが2組）に変換する方法

様々な行列の種類

正方行列：行数n=列数mの行列
（例）

$\boldsymbol{A} =\begin{pmatrix}1&2\\4&5\end{pmatrix}$

単位行列：正方行列において、対角線上の成分が全て1で、その他は全て0である行列。単位行列 $\boldsymbol{I}$ とすると、 $\boldsymbol{AI=IA=A}$ を満たす。（単位行列は、 $\boldsymbol{I}$ だけでなく $\boldsymbol{E}$ と表記されることもある）
（例）

$\boldsymbol{I} =\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}$

逆行列：行列Aに対して、積を取ると単位行列になるような行列。行列の世界での逆数のような存在。右上に添字-1をつけて表す。
$\boldsymbol{AA^{-1}=A^{-1}A=I}$
（例）

$\boldsymbol{A} =\begin{pmatrix}4&2&3\\2&1&1\\3&2&3\end{pmatrix}$

のとき

$\boldsymbol{A^{-1}} =\begin{pmatrix}1&0&-1\\-3&3&2\\1&-2&0\end{pmatrix}$

転置行列：行列Aに対して、行と列を入れ替えた行列のこと。右上に添字Tをつけて表す。
（例）

$\boldsymbol{A} =\begin{pmatrix}1&2\\3&4\end{pmatrix}$

のとき

$\boldsymbol{A^{T}} =\begin{pmatrix}1&3\\2&4\end{pmatrix}$

対角行列：非対角成分が全て0の行列。対角行列同士の積は対角行列になる。対角行列の行列式は、対角成分をかけた値になる。
（例）

$\boldsymbol{A} =\begin{pmatrix}3&0&0\\0&4&0\\0&0&5\end{pmatrix}$

対称行列：主対角線を軸に線対称な行列。行列Aとその転置行列ATが一致する。
（例）

$\boldsymbol{A} =\begin{pmatrix}1&5&-2\\5&2&3\\-2&3&7\end{pmatrix}$

直行行列：行列Aの、転置行列 $\boldsymbol{A^{T}}$ と逆行列 $\boldsymbol{A^{-1}}$ が一致するような行列
$\boldsymbol{A^{T} = A^{-1}}$
（例）

$\boldsymbol{A} =\begin{pmatrix}0&1&0\\1&0&0\\0&0&1\end{pmatrix}$

逆行列の求め方

＜2×2の正方行列の場合＞（メモ）

$\boldsymbol{A} =\begin{pmatrix}a&b\\c&d\end{pmatrix}$ の逆行列 $\boldsymbol{A^{-1}}$ は、

$\boldsymbol{A^{-1}} =1/(ad-bc)\begin{pmatrix}d&-b\\-c&a\end{pmatrix}$

となる

＜掃き出し法＞（メモ）
・元の行列の右側に単位行列を付け加え、行基本変形を繰り返し、左側に単位行列を作るように操作していく方法。

＜逆行列が存在しない時とは？＞

$\boldsymbol{A} =\begin{pmatrix}a&b\\c&d\end{pmatrix}$ とすると、 $\boldsymbol{ad-bc=0}$ となるとき、行列Aは逆行列をもたない。つまり行列式=0の時、逆行列は持たない。

行列式 det(A)

正方行列についてのみ1つの数値が対応する。いわゆる正方行列の「大きさ」のようなもの。

2×2の正方行列の場合は、以下となる。

$\boldsymbol{det(A)} =\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad-bc$

3×3の正方行列の場合

$\boldsymbol{det(A)} =\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix} = a_{11}\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{vmatrix}-a_{21}\begin{vmatrix}a_{12}&a_{13}\\a_{32}&a_{33}\end{vmatrix}+ a_{31}\begin{vmatrix}a_{12}&a_{13}\\a_{22}&a_{23}\end{vmatrix}$

固有値・固有ベクトル

<固有値・固有ベクトルの概要>

ある行列Aに対して、 $\boldsymbol{A\vec{x}=λ\vec{x}}$ となるような特別なベクトル $\vec{x}$ と係数 $\boldsymbol{λ}$ の値がある時、このベクトル $\vec{x}$ を「固有ベクトル」、係数λを「固有値」という。直感的なイメージとしては、行列Aがベクトル $\vec{x}$ を同方向に $\boldsymbol{λ}$ 倍するというイメージ（行列という変換器によって、ベクトルxを向きを変えないまま変換する感じ。）

・固有値は、1つではなく、複数存在する場合もある。
・固有ベクトルは、固有値λに対して、 $\boldsymbol{(A-λI)\vec{x}=0}$ となるようなベクトル $\vec{x}$ を指す。固有値ごとに固有ベクトルは異なる。

＜実際に解いてみる＞

$\boldsymbol{A} =\begin{pmatrix}3&2&0\\0&2&0\\0&0&1\end{pmatrix}$ の固有値・固有ベクトルを求める

手順
① det(A-λI)=0を計算し固有値λを求める
$\boldsymbol{det(A)} =\begin{vmatrix}3-λ&2&0\\0&2-λ&0\\0&0&1-λ\end{vmatrix} = 0$ →これを解いて、λ=3, 2, 1となる。

② 以下の式にλを代入し、ベクトルxを求める

$\begin{pmatrix}3&2&0\\0&2&0\\0&0&1\end{pmatrix}\begin{pmatrix}x_1&x_2&x_3\end{pmatrix}=λ\begin{pmatrix}x_1&x_2&x_3\end{pmatrix}$
λ=3のとき、 $\boldsymbol{\vec{x}=t(1, 0, 0)}$
λ=2のとき、 $\boldsymbol{\vec{x}=t(2, -1, 0)}$
λ=1のとき、 $\boldsymbol{\vec{x}=t(0, 0, 1)}$

固有値分解

固有値を対角線上に並べた行列Λと、固有ベクトルを並べた行列vを考える。

$\boldsymbol{Λ} =\begin{pmatrix}λ_1&0&0\\0&λ_2&0\\0&0&\cdots\end{pmatrix}$ , $\boldsymbol{V} =\begin{pmatrix}\vec{v_1}&\vec{v_2}&\vec{v_3}&\cdots\end{pmatrix}$

このとき

$\boldsymbol{A = VΛV^{-1}}$ が成り立つ。

このように、正方行列を3つの行列の積に変換することを固有値分解という。

＜実際に解いてみる＞

$\boldsymbol{A} =\begin{pmatrix}2&1\\0&6\end{pmatrix}$ を固有値分解せよ

手順
①固有値λを求める。行列式detA=0を解いて、 $\boldsymbol{(2-λ)(6-λ)=0}$ を解き、固有値λ=2,6。
②固有ベクトルxを求める。λ=2のとき、 $\vec{x} = (1,0)$ の定数倍、λ=6のとき、 $\vec{x} = (1, 4)$ の定数倍となる
③ΛとVを求める。 $\boldsymbol{Λ}=\begin{pmatrix}2&0\\0&6\end{pmatrix}$ 、 $\boldsymbol{V}=\begin{pmatrix}1&1\\0&4\end{pmatrix}$ 、 $\boldsymbol{V^{-1}}=\begin{pmatrix}1&-1/4\\0&1/4\end{pmatrix}$
④ $\boldsymbol{A = VΛV^{-1}}$ なので、 $\boldsymbol{A}=\begin{pmatrix}1&1\\0&4\end{pmatrix}\begin{pmatrix}2&0\\0&6\end{pmatrix}\begin{pmatrix}1&-1/4\\0&1/4\end{pmatrix}$

特異値分解

＜概要＞
・固有値計算は正方行列に対してのみであったが、任意の形の行列でも同様の分解をできるようにしたのが特異値分解。
・求め方の流れとしては、ある行列Mの転置行列 $\boldsymbol{M^{-1}}$ との積をとることで正方行列に変換し、その正方行列で固有値分解をする。
　（行列 $\boldsymbol{MM^{-1}}$ と行列 $\boldsymbol{M^{-1}M}$ をそれぞれ固有値分解する）
・ $\boldsymbol{MM^{-1}}$ を固有値分解して得られる固有値が「元の行列Mの特異値の2乗」となっており、固有ベクトルが左特異ベクトルと呼ばれる。
・ $\boldsymbol{M^{-1}M}$ を固有値分解して得られる固有ベクトルを右特異ベクトルと呼ばれる。

＜実際に解いてみる＞

$\boldsymbol{M} =\begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}$ を特異値分解せよ

手順

① $\boldsymbol{MM^{-1}}$ と、 $\boldsymbol{M^{-1}M}$ をそれぞれ固有値分解する。

$\boldsymbol{MM^{-1}}=\begin{pmatrix}14&10\\10&14\end{pmatrix}=\begin{pmatrix}1/\sqrt{2}&-1/\sqrt{2}\\1/\sqrt{2}&1/\sqrt{2}\end{pmatrix}\begin{pmatrix}24&0\\0&4\end{pmatrix}\begin{pmatrix}1/\sqrt{2}&-1/\sqrt{2}\\1/\sqrt{2}&1/\sqrt{2}\end{pmatrix}^{-1}$

$\boldsymbol{M^{-1}M}=\begin{pmatrix}10&6&8\\8&8&8\\6&8&10\end{pmatrix}=\begin{pmatrix}1/\sqrt{3}&1/\sqrt{2}&1/\sqrt{6}\\1/\sqrt{3}&0&-2/\sqrt{6}\\1/\sqrt{3}&-1/\sqrt{2}&1/\sqrt{6}\end{pmatrix}\begin{pmatrix}24&0&0\\0&4&0\\0&0&0\end{pmatrix}\begin{pmatrix}1/\sqrt{3}&1/\sqrt{2}&1/\sqrt{6}\\1/\sqrt{3}&0&-2/\sqrt{6}\\1/\sqrt{3}&-1/\sqrt{2}&1/\sqrt{6}\end{pmatrix}^{-1}$

② $\boldsymbol{MM^{-1}}$ のベクトルの左辺を左特異ベクトル、 $\boldsymbol{M^{-1}M}$ のベクトルの右辺を右特異ベクトルとし、真ん中の固有値行列の平方根をとる

$\boldsymbol{A}=\begin{pmatrix}1/\sqrt{2}&-1/\sqrt{2}\\1/\sqrt{2}&1/\sqrt{2}\end{pmatrix}\begin{pmatrix}2\sqrt{6}&0&0\\0&2&0\end{pmatrix}\begin{pmatrix}1/\sqrt{3}&1/\sqrt{2}&1/\sqrt{6}\\1/\sqrt{3}&0&-2/\sqrt{6}\\1/\sqrt{3}&-1/\sqrt{2}&1/\sqrt{6}\end{pmatrix}^{-1}$

＜応用領域＞
・特異値分解は、画像データの圧縮など次元削減の場面で応用されている技術

2021-09-14

AI実装検定・E資格取得に向けた学習について

１つ前の記事（↓）にも記載しましたが、E資格を受けようとすると事前の認定講座の合格が必須なんですよね・・・。とはいいつつ、来年2月のE資格をひとつの目標として見据えながらも、その前にAI実装検定にトライしてみようかと思っている今日この頃です。

dsnotes.hatenablog.com

と、数日色々なWebページやSNSなどで調べてるところ、以下のラビットチャレンジでは、今E資格向けの講座に申し込むとAI実装検定向けの教材（5万円）が無料になるらしいので、こちらの認定講座を検討してみようかと思っています。

ai999.careers