E資格学習　深層学習 Day1 - 駆け出しからのAI・データサイエンス学習日記

さて、今回は深層学習の基礎と概要について要点をまとめたいと思います。

入力層～中間層
活性化関数
出力層
- 要点まとめ
誤差関数
【実装】2×3×3×1のニューラルネットワークの実装
勾配降下法
誤差逆伝播法（Back Propagation）
- 要点まとめ
- 【実装】

入力層～中間層

要点まとめ
・結局、ディープラーニングは何をやろうとしているのか
　→入力値から目的となる出力値を導く「関数」or「数理モデル」を自動的に学習して構築する仕組み
　　重み[W]とバイアス[b]の最適化が最終目的。

・（例）例えば、最終的に、猫、犬、ねずみといった動物分類を考える。
　　　　入力値：体長、体重、ひげの本数、毛の平均長、耳の大きさ・・・etc
　　　　出力値：猫、犬、ねずみといった各正解ラベルに該当する確率

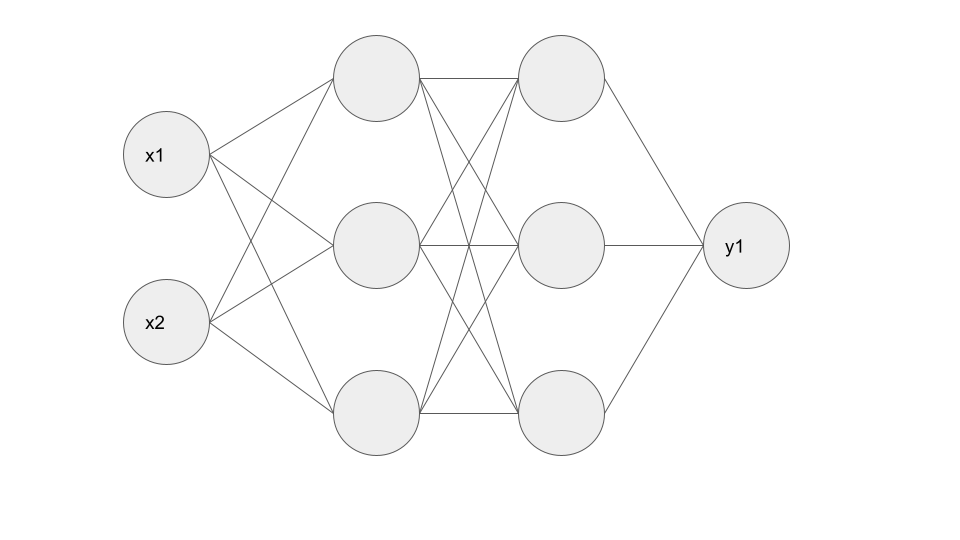
・（例）入力層：2ノード、中間層：3ノード×2層、出力層：1ノードのNN
　　　　 f:id:rakurakura:20220103002312p:plain

活性化関数

要点まとめ

・ニューラルネットワークは非線形の関数であるため複雑な分類・識別タスクに強い。その大きな要因となっているのが活性化関数の存在。
・活性化関数があるおかげで、一部の出力が強く、一部の出力が弱く伝播される。
・主に中間層用の活性化関数：RELU関数、ステップ関数　etc
・主に出力層用の活性化関数：シグモイド関数、ソフトマックス関数　etc

STEP関数

・閾値を超えたら発火する。xがゼロ以上であれば1、そうでなければゼロを返す。
・昨今はあまり使われない。

def step_func(x):
　if x>0:
       return 1
    else:
       return 0

シグモイド関数

・非線形な活性化関数。線形のような直線ではなく、非線形
・値がなだらかな曲線なので、微分が可能。
　ただし、複雑になると、勾配消失問題を引き起こす原因になるため、
　中間層ではあまり使われない。

def sigmoid(x):
  return 1/(1+np.exp(-x))

RELU関数

・ゼロよりも小さい場合はゼロを、大きい場合は入力値をそのまま出力する
・勾配消失を回避できる。

def relu(x):
  return np.maximum(0, x)

Softmax関数

def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T
    x = x - np.max(x) # オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x))

出力層

要点まとめ

・最後の出力層は、人間が欲しい答えに該当する数値（回帰であれば実数値、分類であれば正解ラベルの確率）が出力させる必要がある。

・出力層で使う活性化関数は、中間層で扱う活性化関数のように、特徴抽出ではなくより人間が最終的に扱いやすいように変形させる、という特徴があるため、両者で用いる関数が異なる。

誤差関数

要点まとめ

・出力層で得た出力値と、事前に用意した正解値との差を誤差関数と定義し、この誤差関数を最小化するように最適なパラメータを探索する計算処理→これがNNにおける「学習」そのものである。

・誤差関数を計算する際に、誤差を2乗する理由は？
　→各データと正解との誤差を計算する際に、正負の値が発生すると相殺して全体的な誤差を正しく表現できないため、2乗して正の値として扱うことで正負の相殺を回避する。

・誤差関数を計算する際に、1/2を掛けている理由は？
　→本質的な理由ではなく、便宜上、誤差関数を微分する際に出てくる2を打ち消す効果として1/2をかけている。

・分類問題で使う誤差関数：クロスエントロピー誤差
・回帰問題で使う誤差関数：MSE（平均二乗誤差）

MSE

# 平均二乗誤差
# dが教師データ、yが予測データ
def mean_squared_error(d, y):
    return np.mean(np.square(d - y)) / 2

クロスエントロピー

# dが教師データ、yが予測データ
def cross_entropy_error(y, d):
    # log 0回避用の微小な値を作成
    delta = 1e-7
    
    # 交差エントロピー誤差を計算
    return - np.sum(d* np.log(y + delta))

Softmax関数＋クロスエントロピー

#ソフトマックスとクロスエントロピー誤差の複合関数
def d_softmax_with_loss(d, y):
    batch_size = d.shape[0]
    if d.size == y.size: # 教師データがone-hot-vectorの場合
        dx = (y - d) / batch_size
    else:
        dx = y.copy()
        dx[np.arange(batch_size), d] -= 1
        dx = dx / batch_size
    return dx

【実装】2×3×3×1のニューラルネットワークの実装

イメージ
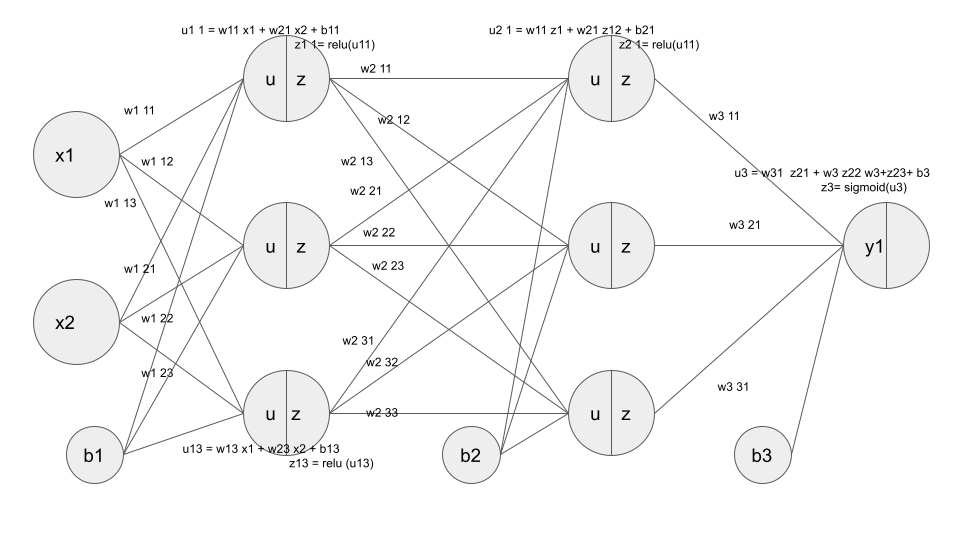
f:id:rakurakura:20220103020050p:plain

#2値分類
#上記に記載した入力層：2層、中間層：3層×2、出力層：1のネットワークを作成する

#シグモイド関数
def sigmoid(x):
    return 1/(1 + np.exp(-x))

#シグモイド関数の微分
def d_sigmoid(x):
    dx = (1.0 - sigmoid(x)) * sigmoid(x)
    return dx

# ReLU関数
def relu(x):
    return np.maximum(0, x)

#ReLU関数の微分
def d_relu(x):
    return np.where( x > 0, 1, 0)


#クロスエントロピー誤差
def cross_entropy_error(d, y):
    if y.ndim == 1:
        d = d.reshape(1, d.size)
        y = y.reshape(1, y.size)
        
    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
    if d.size == y.size:
        d = d.argmax(axis=1)
             
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size


#ネットワークの定義
def init_network():
    network = {}
    network['W1'] = np.random.rand(2, 3)
    network['W2'] = np.random.rand(3, 3)
    network['W3'] = np.random.rand(3, 1)

    network['b1'] = np.random.rand(3)
    network['b2'] =np.random.rand(3)
    network['b3'] =np.random.rand(1)

    return network

#ネットワーク
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'],network['W3']
    b1, b2, b3 = network['b1'], network['b2'],network['b3']

    # 隠れ層の総入力
    u1 = np.dot(x, W1) + b1

    # 隠れ層1の総出力
    z1 = relu(u1)

    # 隠れ層２層への総入力
    u2 = np.dot(z1, W2) + b2

    # 隠れ層2の出力
    z2 = relu(u2)
    
    u3 = np.dot(z2, W3) + b3
    z3 = sigmoid(u3)

    y = z3    
    
    return y, z1

# 入力値
x = np.array([1., 2.])

# 目標出力
d = np.array([1])
network =  init_network()
y, z1 = forward(network, x)
# 誤差
loss = cross_entropy_error(d, y)

勾配降下法

要点まとめ

・深層学習でパラメータを最適化するために用いられる手法＝勾配降下法
・通常の勾配降下法は、バッチ学習のようにデータを全て準備し、全て使って学習するイメージ。パラメータの更新式は、 $w_{t+1} = w_{t} - ε∇E$ で表される。
・バリエーションとして、確率的勾配降下法（SGD）とミニバッチ勾配降下法がある。
・バッチ処理なので、大量のデータを扱う際には、かなり計算コストが高くなる。

確率的勾配降下法

・バッチ学習とは異なり、オンライン学習（学習データが入ってくるたびに、都度パラメータを更新し学習を進めていく方法）
・ $w_{t+1} = w_{t} - ε∇E_{n}$ で表される。（Eの添字にnが入っている点がバッチ学習と違うところ！）

ミニバッチ勾配降下法

・確率的勾配降下法のメリットを損なわず、大量のデータを「小分け」することで扱えるようにした手法。この小分けにしたデータ集合をミニバッチと呼ぶ。
・10万枚を500枚ずつに小分けすると2000個のバッチができあがる。
・500枚単位での誤差が2000個分集まると2000で割ることで平均的な誤差が求まる。
・小分けしたデータを並列処理することで、バッチ処理とは異なり計算資源を有効利用できるメリットもある。（SIMD並列化：single instruction multi data）
$w_{t+1} = w_{t} - ε∇E_{t}$ で表される。

学習のイメージ

・エポックの進行：t → t+1 → t+2 とすると、
・重みの値　： $w_t → w_{t+1} → w_{t+2}$ と変化する
・変化量　　： $-ε∇E_{t} → -ε∇E_{t+1}$

誤差逆伝播法（Back Propagation）

要点まとめ

・上記のような、重みの更新の際に必要となる∇Eをどのように求めるのか？
→誤差関数の微分を用いることで更新できるが、重みの数が膨大になると微分の計算も膨大になり負荷が大きくなるので、数値微分だと限界。そこで、微分の連鎖律の性質を活用することで、「解析的に」計算することができる誤差逆伝播法が用いられる。

【実装】

# 誤差逆伝播
def backward(x, d, z1, y):
    grad = {}
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']

    # 出力層でのデルタ（Eをyで微分したもの）
    delta2 = mean_squared_error(d, y)

    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)

    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)

    # 出力層でEをyで微分した結果「delta2」と、yをuで微分した結果を掛けている
    delta1 = np.dot(delta2, W2.T) * d_sigmoid(z1)

    delta1 = delta1[np.newaxis, :]

    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    x = x[np.newaxis, :]

    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)
    
　return grad

$\frac {∂E}{∂y} \cdot \frac {∂y}{∂u}$ の部分は以下のコードで表している。

delta1 = np.dot(delta2, W2.T) * d_sigmoid(z1)