E資格学習　深層学習 Day2 ① 勾配消失問題〜最適化手法〜過学習 - 駆け出しからのAI・データサイエンス学習日記

勾配消失問題
最適化手法
過学習

勾配消失問題

要点まとめ

ニューラルネットワークの学習がうまくいかなくなる原因の一つ。入力層に近いパラメータでは学習してもほとんど変わらない状態になる。中間層が多くなると起こりやすい。

→なぜか？中間層が多くなると誤差逆伝播における微分の回数が増える。微分値に0~1の間の数値があると、掛け合わすたびに非常に小さな数になってしまうから。

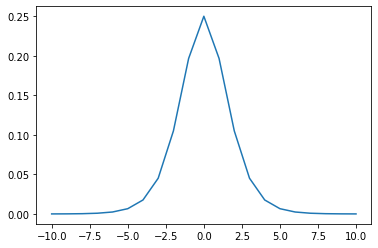
→特にシグモイド関数は、勾配消失を起こす要因となる活性化関数である。シグモイドは微分すると、最大でも0.25となる。（下記）

#シグモイド関数の実装
def sigmoid(x):
    s = 1/(1+np.exp(-x))
    return s

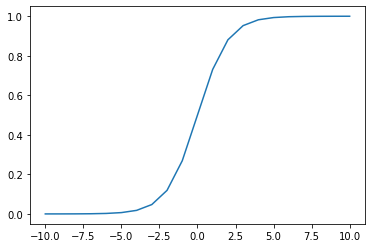
f:id:rakurakura:20220103123928p:plain

#シグモイド関数の微分
def d_sigmoid(x):
    s_d = (1-sigmoid(x))*sigmoid(x)
    return s_d

f:id:rakurakura:20220103123946p:plain

勾配消失を回避する3つの方法

活性化関数の選択：シグモイドではなく、ReLU関数を使う。
初期値を工夫する：重みパラメータ $w$ は、乱数でランダムな初期値を与えるが、この与え方を工夫することで勾配消失を回避できる。シグモイドのようなS字カーブ型の場合は、Xavierの初期値を使う。Xavierでは、重みの要素を、前層のノード数の平方根で割った値を使うことで、良い感じに微分値のばらつきと表現力が保持される。
バッチ正規化：ミニバッチの単位で、入力値のデータの偏りを抑制する手法。メリットとして、中間層の学習が安定しスピードアップする・極端なばらつきがなくなり、過学習が抑制できる。

【実装】Xavier/ He 初期値の設定方法

#Xavierの初期値
network["W1"] = np.randdom.randn(input_layer_size, hidden_layer_size) / np.sqrt(input_layer_size)
network["W2"] = np.randdom.randn(hidden_layer_size, output_layer_size) / np.sqrt(hidden_layer_size)

ReLU関数などのS字カーブではない場合は、Heの初期値設定を行うと良い。
Xavierと違うのは、 $\sqrt 2/n$ で割っているところ。

#Heの初期値
network["W1"] = np.randdom.randn(input_layer_size, hidden_layer_size) / np.sqrt(input_layer_size) * np.sqrt(2)
network["W2"] = np.randdom.randn(hidden_layer_size, output_layer_size) / np.sqrt(hidden_layer_size) * np.sqrt(2)

（メモ）重みの初期値をゼロにしてしまうと、すべての重みの値が均一に更新されてしまうので、ニューラルネットワークとして機能が果たせない点に注意。活性化関数によって初期値の与え方は使い分けるべし。

【実装】バッチ正規化レイヤー

# バッチ正則化 layer
class BatchNormalization:
    def __init__(self, gamma, beta, momentum=0.9, running_mean=None, running_var=None):
        self.gamma = gamma #スケール関数
        self.beta = beta #オフセット
        self.momentum = momentum
        self.input_shape = None

        self.running_mean = running_mean #テスト時の平均
        self.running_var = running_var  
        
        # backward時に使用する中間データ
        self.batch_size = None
        self.xc = None
        self.std = None
        self.dgamma = None
        self.dbeta = None

    def forward(self, x, train_flg=True):
        if self.running_mean is None:
            N, D = x.shape
            self.running_mean = np.zeros(D)
            self.running_var = np.zeros(D)
                        
        if train_flg:
            mu = x.mean(axis=0) # 平均
            xc = x - mu # xをセンタリング
            var = np.mean(xc**2, axis=0) # 分散
            std = np.sqrt(var + 10e-7) # スケーリング
            xn = xc / std
            
            self.batch_size = x.shape[0]
            self.xc = xc
            self.xn = xn
            self.std = std
            self.running_mean = self.momentum * self.running_mean + (1-self.momentum) * mu # 平均値の加重平均
            self.running_var = self.momentum * self.running_var + (1-self.momentum) * var #分散値の加重平均
        else:
            xc = x - self.running_mean
            xn = xc / ((np.sqrt(self.running_var + 10e-7)))
            
        out = self.gamma * xn + self.beta 
        
        return out

最適化手法

要点まとめ

勾配降下法における、 $w_{t+1} ← w_{t} - ε∇E$ のεの最適化の手法。オプティマイザーという。
学習率が大きいと発散し正解にたどり着かない。学習率が小さい場合は、大域局所最適値に収束しづらい。
モメンタム、Adagrad、RMSProp、Adamの主に4つの手法があり、昨今はAdamが定番になっている。

モメンタム

　 $V_{t} = μV_{t-1} - ε∇E$
　 $w_{t+1} = w_{t} +V_{t}$

前回の重みを考慮し、慣性の考え方を取り入れている。
最初は動きが遅いが谷間についてから最も低い位置にいくまでの時間が早く、大域局所最適値にたどり着きやすい。移動平均のようは進み方をする。

self.v[key] = self.momentum * self.v[key] -self.learning_rate * grad[key]
params[key] += self.v[key]

Adagrad

　 $h_{0} = θ$
　 $h_{t} = h_{t-1} +(∇E)^2$
　 $w_{t+1} = w_{t} -ε \cdot \frac{1}{\sqrt {h_{t}} + θ} \cdot ∇E$

これまでの学習履歴をh に蓄積させておくイメージ。
緩やかな勾配にスムーズに学習が進みやすいが、大域局最適値にたどりつきにくい。
鞍点のような状態では学習が進まなくなる。

self.h[key] = np.zeros_like(val) #なにかしらの値で初期化
self.h[key] += grad[key] * grad[key] #計算した勾配の2乗を保持しておく
params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7) #現在の重みを適応させた学習率で更新

RMSProp

　 $h_{t} = αh_{t-1} +(1-α)(∇E)^2$
　 $w_{t+1} = w_{t} -ε \cdot \frac{1}{\sqrt {h_{t}} + θ} \cdot ∇E$

Adagradの改良版。重みの更新式は同じだが、前回の経験をどの程度活かすかを調整する係数α（0~1の値 decay rate）が追加。
Adagradで難しかった鞍点問題をスムーズに解消できるようになった。
εやdecay rateは人間が最初に設定するハイパーパラメータ。

self.h[key] *= self.decay_rate #数式でのαをhにかける。
self.h[key] += (1-self.decay_rate) * grad[key] * grad[key] 
params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7) #Adagradと同じ

Adam

モメンタムとRMSPropのメリットを孕んだアルゴリズム

　 $g_{t} = ∇_{θ}f_{t} (θ_{t-1})$
　 $m_{t} = β_1 \cdot m_{t-1}+(1-β_1）\cdot g_{t}$
　 $v_{t} = β_2 \cdot v_{t-1}+(1-β_2）\cdot g_{t}^2$
　 $\hat{m_{t}} = m_{t} / (1-β_1^t)$
　 $\hat{v_{t}} = v_{t} / (1-β_2^t)$
　 $w_{t} = w_{t-1} - α \cdot \hat{m_{t}} / (\sqrt {\hat{v_{t}} }+ ε)$

 m[key] = np.zeros_like(network.params[key])
 v[key] = np.zeros_like(network.params[key])
            
 m[key] += (1 - beta1) * (grad[key] - m[key])
 v[key] += (1 - beta2) * (grad[key] ** 2 - v[key])            
 network.params[key] -= learning_rate_t * m[key] / (np.sqrt(v[key]) + 1e-7)

過学習

要点まとめ

訓練データに特化して学習してしまい、テスト誤差が収束しなくなること
原因としては、入力データ数が少ない割に大きなニューラルネットワーク（パラメータ数が多い）場合に起こり得る。パラメータ値が適切ではない（特定の重みが大きい値をとってしまっている）。ノード数が多すぎるなどが挙げられる。＝ニューラルネットワークの自由度が高すぎることが大きな要因になる。

正則化手法

過学習を抑えるアプローチとして、ニューラルネットワークの自由度に制限を与えることで対応する。過学習が起きている時、重要な重みが大きくなるが、一部の重みが極端に大きすぎることで過学習になっていることがある。そこで、重みを大きくなりすぎないような工夫としてL1、L2正則化によって、Weight Decayを実施する。

Weight Decay （重み減衰）：過学習が起こりそうな重みの大きさ以下にコントロールし、かつ重みの大きさにばらつきを出す。具体的には、誤差関数にPノルムを加える。

L1正則化：ラッソ回帰　L2正則化：リッジ回帰　では、pノルムというベクトルの距離を使う。p1ノルムではマンハッタン距離（横方向と縦方向を足すだけ）、p2ノルムはユークリッド距離（二乗して平方根する直線距離）で計算する。

重みのpノルムを計算し、誤差関数に正則化項として加えるイメージ。誤差関数の形を正則化項を足し合わせることで、変形させ、最適解の場所をずらすことで、過学習となるような最適解に陥らないようにする効果がある。

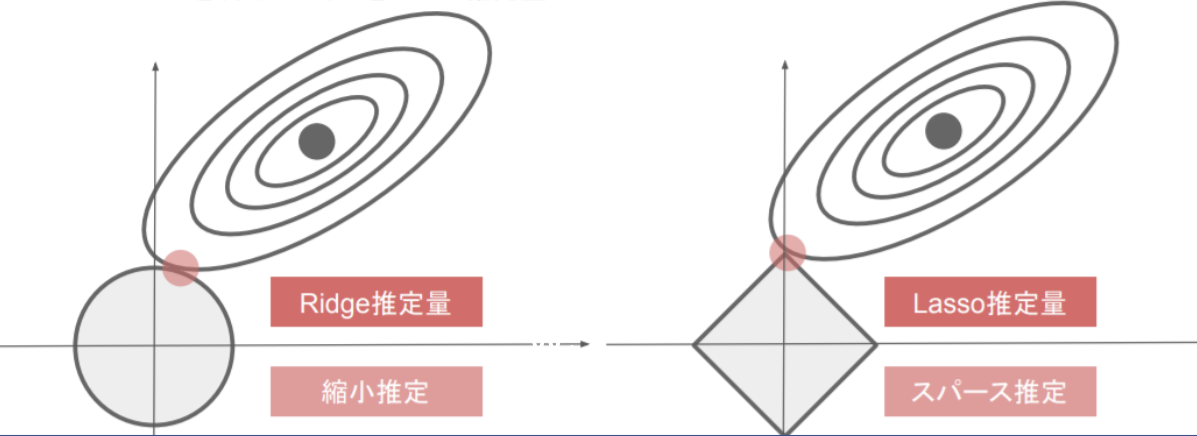
f:id:rakurakura:20220103150103p:plain

↑ 左がL2正則化、右がL1正則化
（誤差関数の等高線のイメージ）

【実装】L1正則化、L2正則化

#p1ノルムを使った正則化（L1正則化）部分抜粋
    for idx in range(1, hidden_layer_num+1):
        grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * np.sign(network.params['W' + str(idx)])
        grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
        network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
        network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]        
        weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))#絶対値をとっている

    loss = network.loss(x_batch, d_batch) + weight_decay

#p2ノルムを使った正則化（L2正則化）部分抜粋
for idx in range(1, hidden_layer_num+1):
        grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * network.params['W' + str(idx)]
        grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
        network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
        network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]        
        weight_decay += 0.5 * weight_decay_lambda * np.sqrt(np.sum(network.params['W' + str(idx)] ** 2)) #2乗の平方根をとっている

    loss = network.loss(x_batch, d_batch) + weight_decay

ドロップアウト

ノード数が多いことで過学習が起こる問題に対して、ランダムにノードを削除して学習させる手法がドロップアウト。データ量を変化させずに、異なるモデルを学習させているアンサンブル学習ともいえる。データのバリエーションを増やすことで過学習の抑止につながる。

・ドロップアウトとは異なり、ドロップコネクトという手法もあるが、これはノードは削除せずに、重みパラメータを削除することで、ノード間の接続のバリエーションを変える手法。

#ネットワークの定義
class MultiLayerNet:
    '''
    input_size: 入力層のノード数
    hidden_size_list: 隠れ層のノード数のリスト
    output_size: 出力層のノード数
    activation: 活性化関数
    weight_init_std: 重みの初期化方法
    weight_decay_lambda: L2正則化の強さ
    use_dropout: ドロップアウトの有無
    dropout_ratio: ドロップアウト率
    use_batchnorm: バッチ正規化の有無
   '''
   def __init__(self, input_size, hidden_size_list, output_size, activation='relu', weight_init_std='relu', weight_decay_lambda=0,
                 use_dropout = False, dropout_ratio = 0.5, use_batchnorm=False):
        self.input_size = input_size
        self.output_size = output_size
        self.hidden_size_list = hidden_size_list
        self.hidden_layer_num = len(hidden_size_list)
        self.use_dropout = use_dropout
        self.weight_decay_lambda = weight_decay_lambda
        self.use_batchnorm = use_batchnorm
        self.params = {}

        # 重みの初期化
        self.__init_weight(weight_init_std)

        # レイヤの生成
        activation_layer = {'sigmoid': layers.Sigmoid, 'relu': layers.Relu}
        self.layers = OrderedDict()
        for idx in range(1, self.hidden_layer_num+1):
            self.layers['Affine' + str(idx)] = layers.Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])
            if self.use_batchnorm:
                self.params['gamma' + str(idx)] = np.ones(hidden_size_list[idx-1])
                self.params['beta' + str(idx)] = np.zeros(hidden_size_list[idx-1])
                self.layers['BatchNorm' + str(idx)] = layers.BatchNormalization(self.params['gamma' + str(idx)], self.params['beta' + str(idx)])
                
            self.layers['Activation_function' + str(idx)] = activation_layer[activation]()
            
            if self.use_dropout:
                self.layers['Dropout' + str(idx)] = layers.Dropout(dropout_ratio)

        idx = self.hidden_layer_num + 1
        self.layers['Affine' + str(idx)] = layers.Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])

        self.last_layer = layers.SoftmaxWithLoss()

    def __init_weight(self, weight_init_std):
        all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
        for idx in range(1, len(all_size_list)):
            scale = weight_init_std
            if str(weight_init_std).lower() in ('relu', 'he'):
                scale = np.sqrt(2.0 / all_size_list[idx - 1])  # ReLUを使う場合に推奨される初期値
            elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
                scale = np.sqrt(1.0 / all_size_list[idx - 1])  # sigmoidを使う場合に推奨される初期値
            self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
            self.params['b' + str(idx)] = np.zeros(all_size_list[idx])

    def predict(self, x, train_flg=False):
        for key, layer in self.layers.items():
            if "Dropout" in key or "BatchNorm" in key:
                x = layer.forward(x, train_flg)
            else:
                x = layer.forward(x)

        return x

    def loss(self, x, d, train_flg=False):
        y = self.predict(x, train_flg)

        weight_decay = 0
        for idx in range(1, self.hidden_layer_num + 2):
            W = self.params['W' + str(idx)]
            weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W**2)

        return self.last_layer.forward(y, d) + weight_decay

    def accuracy(self, X, D):
        Y = self.predict(X, train_flg=False)
        Y = np.argmax(Y, axis=1)
        if D.ndim != 1 : D = np.argmax(D, axis=1)

        accuracy = np.sum(Y == D) / float(X.shape[0])
        return accuracy

    def gradient(self, x, d):
        # forward
        self.loss(x, d, train_flg=True)

        # backward
        dout = 1
        dout = self.last_layer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 設定
        grads = {}
        for idx in range(1, self.hidden_layer_num+2):
            grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.params['W' + str(idx)]
            grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db

            if self.use_batchnorm and idx != self.hidden_layer_num+1:
                grads['gamma' + str(idx)] = self.layers['BatchNorm' + str(idx)].dgamma
                grads['beta' + str(idx)] = self.layers['BatchNorm' + str(idx)].dbeta

Dropoutのクラスを生成する

#Dropoutのクラスを生成
class Dropout:
    def __init__(self, dropout_ratio=0.5):
        self.dropout_ratio = dropout_ratio
        self.mask = None

    def forward(self, x, train_flg=True):
        if train_flg:
            self.mask = np.random.rand(*x.shape) > self.dropout_ratio
            return x * self.mask
        else:
            return x * (1.0 - self.dropout_ratio)

    def backward(self, dout):
        return dout * self.mask

use_dropout = True
dropout_ratio = 0.15

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10, weight_decay_lambda=weight_decay_lambda, use_dropout = use_dropout, dropout_ratio = dropout_ratio)